Emerging Model Architectures and the Possibility of Cheaper, More Energy-Efficient AI Training

As AI continues to advance, several pressing challenges are becoming increasingly evident. The high cost, huge energy demands, and limited availability of computational resources pose significant barriers to widespread adoption and innovation. These issues are further compounded by reliance on third-party LLM providers, raising serious concerns about security, privacy, and control. Current models can also lack diversity and specialization, which limits their effectiveness in downstream tasks. While workarounds such as Retrieval-Augmented Generation can help customize these models, training them on custom data can be a more powerful and elegant way to fully leverage proprietary information and develop competitive, tailored AI products and services.
In this study, we explore the use of 1.58 Bit LLMs as a potential solution. Our approach leverages a practical evaluation of scaling laws to demonstrate that 1.58 Bit LLMs can offer significant improvements over full-precision FP16 models in terms of latency, memory usage, throughput, and energy efficiency.
This project is a continuation of the research presented in the following published AI paper ARXIV.
The 1.58-bit LLM represents a groundbreaking approach to optimizing Large Language Models by encoding parameters using a ternary set of values (-1, 0, 1), effectively reducing weight precision to 1.58 bits. This innovative method not only matches the performance of full-precision FP16 models in terms of perplexity and task effectiveness but also demonstrates significant improvements in latency, memory usage, throughput, and energy consumption. These advancements are particularly crucial given the growing concerns about the deployment challenges and environmental impacts associated with increasingly large LLMs.
Built on the Llama architecture, the 1.58-bit LLM offers a more efficient alternative to traditional post-training quantization methods. By focusing on optimizing matrix multiplication, the most computationally expensive task in LLMs, this approach replaces floating-point operations with integer addition, resulting in substantial energy savings. Furthermore, the use of 8-bit activations enables more efficient processing of longer sequences. As model sizes continue to grow, the efficiency gains of the 1.58-bit LLM become even more pronounced, offering significant reductions in memory usage and energy consumption compared to FP16 models.
Scaling laws are essential tools for predicting the performance of LLMs as we increase their size, training data, and computational resources. They provide empirical relationships that help estimate the capabilities of models that are too large to train in practice, offering insights into how performance metrics improve with scaling. Given the significant computational demands of training very large LLMs, scaling laws guide researchers in making informed decisions about resource allocation and future model design, effectively bridging the gap between current capabilities and the potential of even larger, more advanced models.
We created customized 1.58 and FP16 variants of the Llama 2 model and conducted multiple training sessions at different parameter sizes to derive scaling laws for each variant. These laws allowed us to forecast the performance of our models at larger sizes, which we then compared to evaluate how scaling affects their performance.
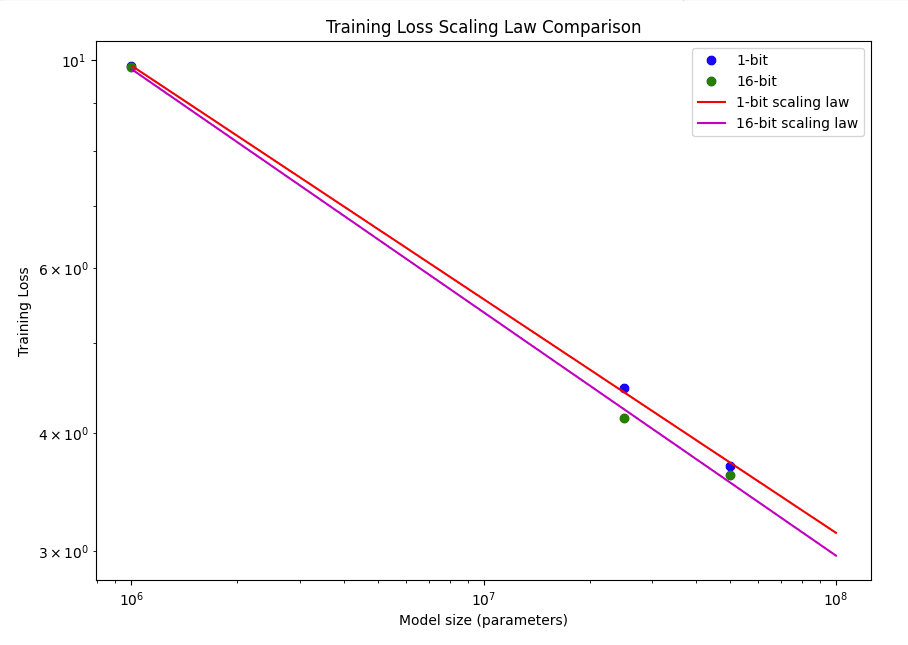
Our research has revealed that the 1.58-bit model exhibits remarkable performance, defying expectations given its extremely low precision. The loss rate of the 1.58-bit model remains on par with that of the FP 16-bit model as the parameter size increases. This striking result demonstrates that the 1.58-bit model retains competitive performance on downstream tasks, suggesting that it effectively manages to balance precision and efficiency.
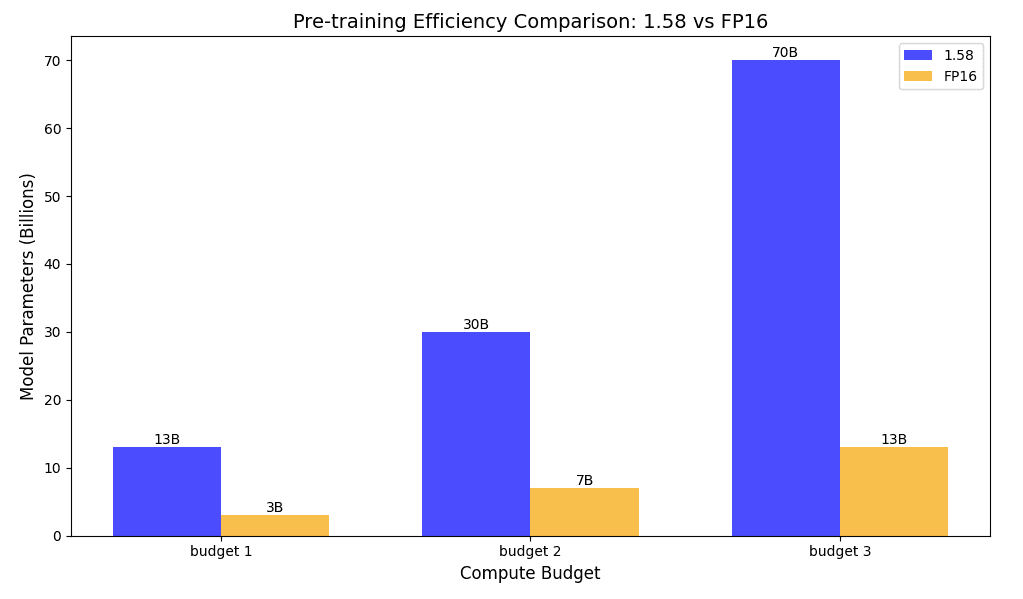
We see impressive results with the 1.58-bit model, which demonstrates a significant leap in memory and energy efficiency compared to its FP16 counterpart. When we applied our GPU metrics to the scaling laws, it became evident that as the model size increases, the 1.58-bit variant delivers an impressive reduction in both memory footprint and energy consumption. This efficiency gain is not just incremental but transformative, enabling the deployment of larger models with lower resource overhead, thereby paving the way for scalable AI solutions that are both cost-effective and environmentally friendly.